Time and Space Complexity

Time and Space Complexity

🧠 Classification of Data Structures

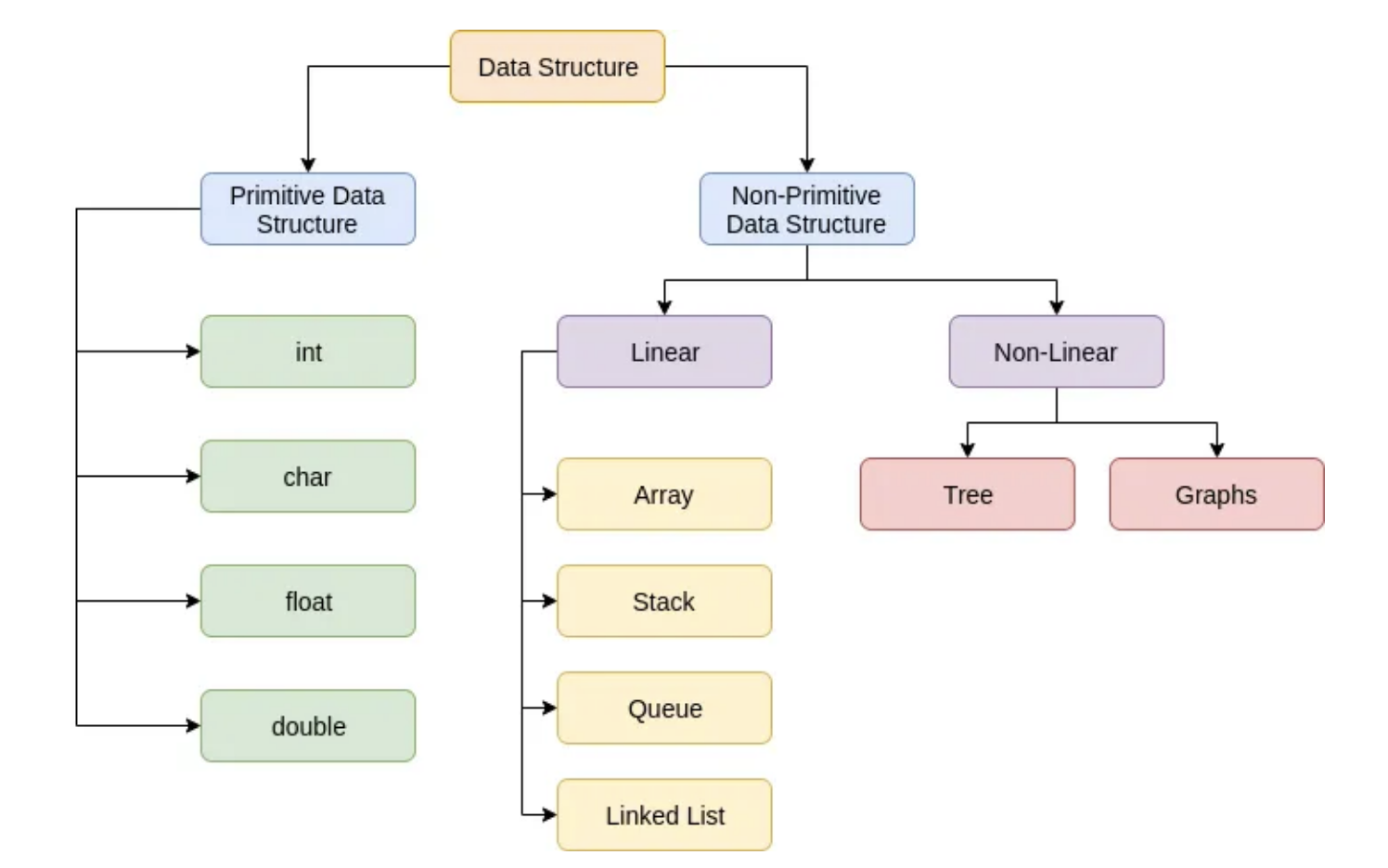
TC and SC Basics
  • Data Structures are categorized into Primitive and Non-Primitive types, where primitive types (like int, char, float, double) are the basic building blocks and are directly supported by most programming languages and hardware.
  • Non-Primitive Data Structures are further divided into Linear and Non-Linear, where linear structures like Arrays, Stacks, Queues, and Linked Lists store elements sequentially — ideal for iteration, searching, or order-based operations.
  • Non-Linear Structures like Trees and Graphs model complex relationships, like file systems, org charts, and web links.
  • Understanding this hierarchy helps in pattern recognition during problem solving, e.g., a queue for BFS, a tree for recursion-heavy problems, and graphs for traversal/connectivity.

🧠 What is Time and Space Complexity?

1. Time Complexity (TC):

Time complexity measures how the number of operations grows with input size n.

Examples:

  • O(1): Constant time
  • O(n): Linear
  • O(n^2): Quadratic
  • O(log n): Logarithmic

✅ Focus on dominant term and worst-case complexity.

2. Space Complexity (SC):

Space complexity measures how much extra memory is used.

Examples:

  • O(1): Constant extra space
  • O(n): Hash map or array use
  • O(n) call stack in recursion

📊 Time and Space Complexity Cheat Sheet

ComplexityNameFeasible Input Size (n)
O(1)ConstantInstant
O(log n)LogarithmicUp to 10^18+
O(n)LinearUp to 10^6–10^7
O(n log n)LinearithmicUp to 10^5–10^6
O(n^2)QuadraticUp to 10^3
O(n^3)CubicUp to 100
O(2^n)ExponentialUp to 20–25
O(n!)FactorialUp to 10

🎯 How to Decide the Required TC/SC for an Interview Problem?

  • n ≤ 10: Acceptable TC: O(n!), O(2^n) — use brute force or backtracking
  • n ≤ 25: Acceptable TC: O(2^n) — bitmasking, subsets
  • n ≤ 100: Acceptable TC: O(n^3) — triple nested loops
  • n ≤ 1000: Acceptable TC: O(n^2) — dynamic programming
  • n ≤ 1e5: Acceptable TC: O(n log n) or O(n) — sorting, sliding window
  • n ≤ 1e6+: Acceptable TC: O(n), O(log n) — hashing, two pointers

📈 Big-O Complexity Chart

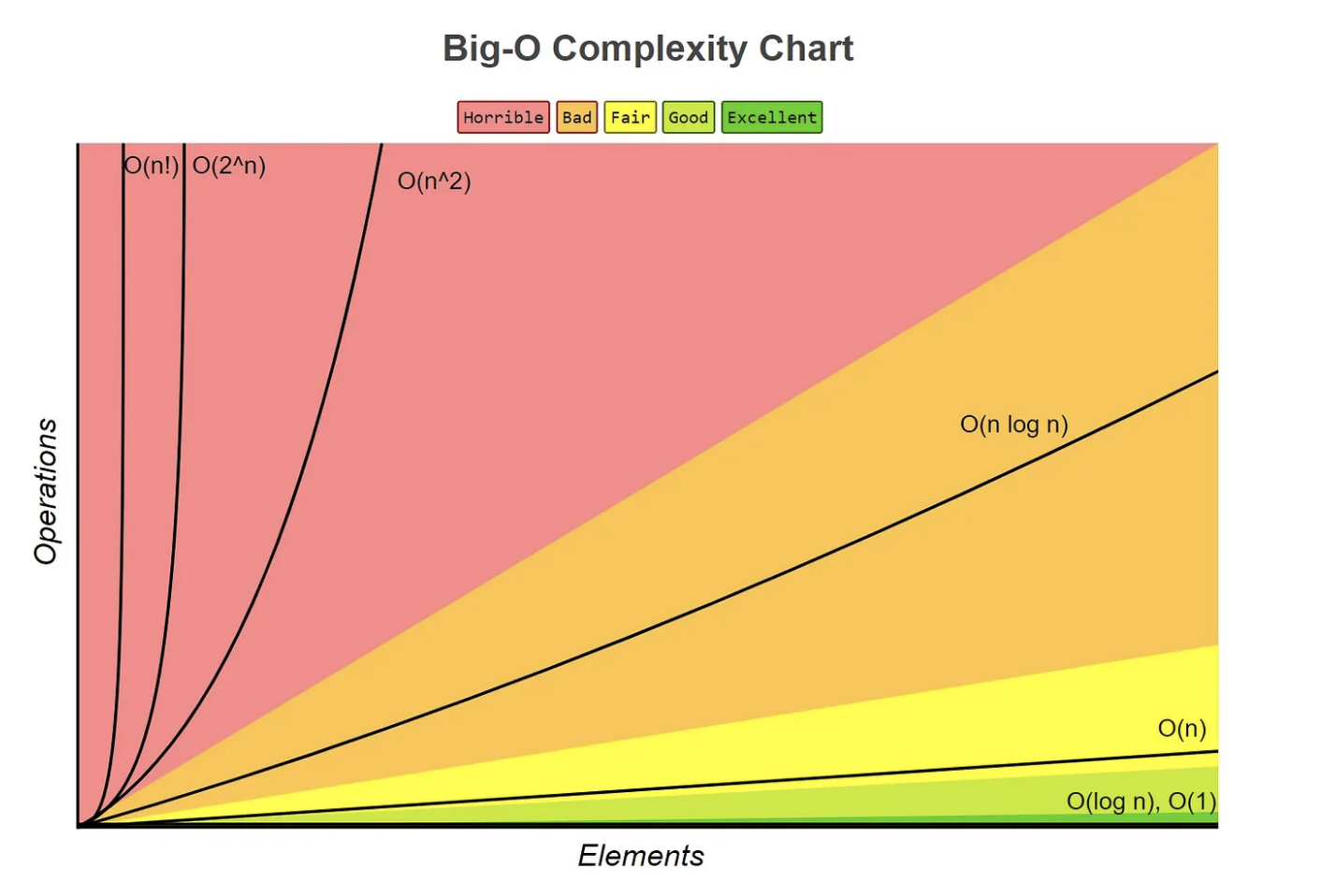
TC and SC Basics

Color code:

  • ✅ Excellent: O(1), O(log n)
  • 🟡 Good to Fair: O(n), O(n log n)
  • 🔴 Bad to Horrible: O(n^2), O(2^n), O(n!)

🌟 Highlights from the Article

  • Big O notation (aka asymptotic analysis) measures how many operations an algorithm takes to complete — helping compare efficiency across solutions.
  • ⚠️ There is no single fastest algorithm in all scenarios — performance varies depending on input state and best/worst-case paths.

📚 Want to go deeper?
Check out this excellent breakdown on Medium

Learning Big-O and complexity patterns early helps you write optimized code and choose the right approach in interviews.

✅ Practice Tip

Try analyzing the complexity of your solution before you code. Over time, this habit will lead to more efficient algorithms and better problem-solving instincts.